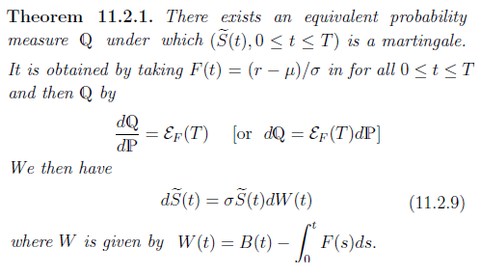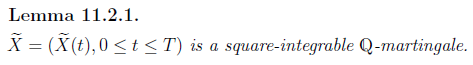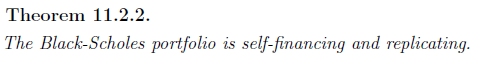Masters Stochastic Processes and FInance Karteikarten am Chapter 11: The Black-Scholes Model, erstellt von mho1 am 07/06/2015.
Angeheftet an
6
0
0
Keine Merkmale angegeben
|
|
Erstellt von mho1
vor mehr als 9 Jahre
|
|
Schließen