Key facts and formulae which must be known for the WJEC Core 2 examination.
|
Erstellt von Daniel Cox
vor mehr als 8 Jahre
|
|
Schließen
|
|
Erstellt von Daniel Cox
vor mehr als 8 Jahre
|
|
\[\log_a x+\log_a y = ?\]
\[\log_a x-\log_a y = ?\]
\[k \log_a x = ?\]
State the sine rule
True or false?
\[\log_a\left (xy^k \right )=k \log_a\left ( xy \right )\]
What is the trigonometric formula for the area of a triangle?
What is the Pythagorean trigonometric identity?
(Hint: it involves \(\sin^2 x\) and \(\cos^2 x\)
If \(y=a^x\), then \(x=?\)
State the cosine rule
\[\log_a a =?\]
\[\log_a 1 =?\]
State an identity relating \(\sin x\), \(\cos x\) and \(\tan x\)
How many degrees is \(\pi\) radians?
Formula for the area of a sector?
Formula for the length of an arc?
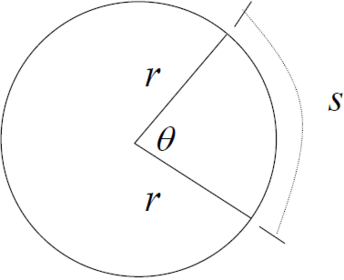
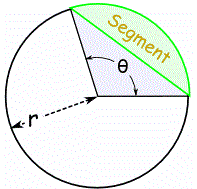
How would you find the area of a segment of a circle?
Formula for the \(n\)th term of an arithmetic sequence...
[given in the formulae booklet]
Formula for the sum of the first \(n\) terms of an arithmetic sequence...
[given in the formulae booklet]
Formula for the \(n\)th term of a geometric sequence...
[given in the formulae booklet]
Formula for the sum of the first \(n\) terms of a geometric sequence...
[given in the formulae booklet]
Formula for the sum to infinity of a convergent geometric series (one where \(\left | r \right |<1\))
[given in the formulae booklet]
\[\int ax^n \, dx=\, ?\]
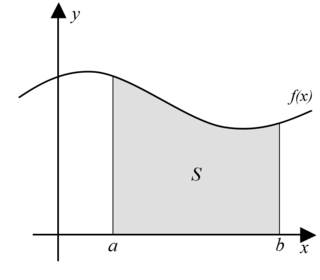
How would you find this shaded area?
General equation of a circle, centre \(\left ( a,b \right )\) and radius \(r\)
If we are given \(\frac{dy}{dx}\) or \(f'(x)\) and told to find \(y\) or \(f(x)\), we need to...
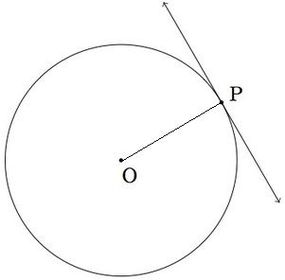
What is the angle between the tangent and radius at \(P\)?
What does the graph of \(y=a^x\) look like?
Where does it cross the axes?
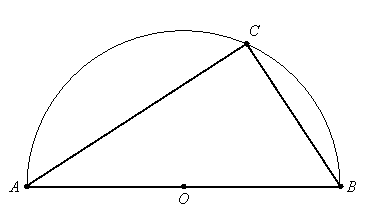
This is a triangle inside a semicircle, where one side of the triangle is the diameter of the circle.
What is the size of angle \(C\)?
Draw the graph of \(y=\sin x\) for \(0\leq x \leq 2\pi\)
Draw the graph of \(y=\cos x\) for \(0\leq x \leq 2\pi\)
Draw the graph of \(y=\tan x\) for \(0\leq x \leq 2\pi\)
Differentiation is the reverse of ...?
Integration is the reverse of ...?
What is the condition for two circles to touch externally?
What is the condition for two circles to touch internally?
If we draw the perpendicular bisector of any chord on a circle, which point will it definitely go through?
