Key facts and formulae which must be known for the WJEC Statistics 1 examination.
Angeheftet an
111
1
0
Keine Merkmale angegeben
|
|
Erstellt von Daniel Cox
vor mehr als 8 Jahre
|
|
Schließen
|
|
Erstellt von Daniel Cox
vor mehr als 8 Jahre
|
|

What does it mean if events A and B are mutually exclusive?
Also, \(P(A\cap B)=?\)
What does it mean if events A and B are independent?
Also, \(P(A\cap B)=?\)
\[P(A|B)=?\] (there is a rearranged version of this given in the formulae book)
If events A and B are independent, then \(P(A|B)=?\)
If events A and B are independent, then \(P(B|A)=?\)
The addition law for events A and B is \[P(A\cup B)=?\] (given in formulae book)
\[P(A')=?\]
For events A and B that are NOT independent, \[P(A\cap B)=?\]
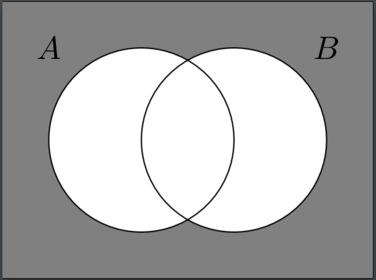
Describe this shaded area using set notation
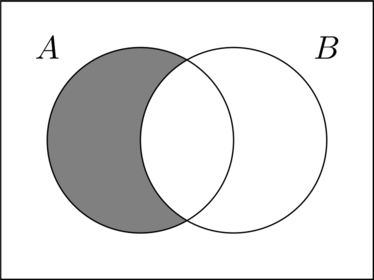
What is a sample space?
How many unordered samples of size \(r\) can be taken from a collection of \(n\) objects?
For any discrete random variable \(X\),\[\text{E}(aX + b) = ?\]
For any discrete random variable \(X\),\[\text{Var}(aX + b) = ?\]
For a discrete random variable \(X\) taking values \(x_i\) with probabilities \(p_i\), \[\text{E}(X)=?\] (given in formulae book)
For a discrete random variable \(X\) taking values \(x_i\) with probabilities \(p_i\), \[\text{Var}(X)=?\] (given in formulae book)
Describe this shaded area using set notation
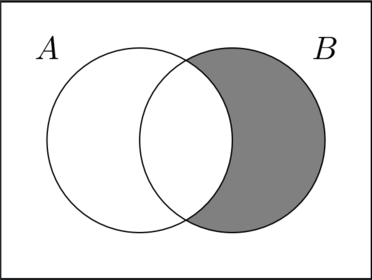
Give the formula for the expected value of a function \(g(X)\) of a discrete random variable
(given in formulae book)
\[X \sim B(n,p)\] \(\text{E}(X)=?\)
(given in formulae book)
\[X \sim B(n,p)\] \(\text{Var}(X)=?\)
(given in formulae book)
\[X \sim Po(\lambda)\] \(\text{E}(X)=?\)
(given in formulae book)
\[X \sim Po(\lambda)\] \(\text{Var}(X)=?\)
(given in formulae book)
Describe this shaded area using set notation
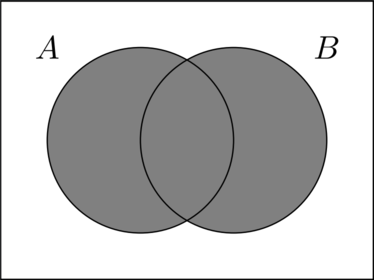
How would you use the Binomial or Poisson tables to find \(P(X=n)\)?
How would you use the Binomial or Poisson tables to find \(P(X>n)\)?
How would you use the Binomial or Poisson tables to find \(P(X\geq n)\)?
How would you use the Binomial or Poisson tables to find \(P(X<n)\)?
For a continuous probability distribution, how are \(f(x)\) and \(F(x)\) related?
If \(q\) is the lower quartile of a continuous random variable \(X\) with cumulative distribution function \(F\), then \[F(q)=?\]
Describe this shaded area using set notation
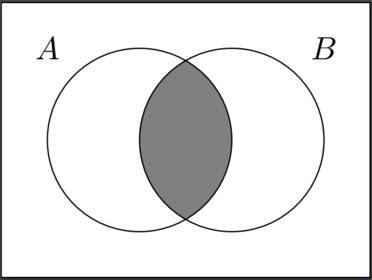
If \(m\) is the median of a continuous random variable \(X\) with cumulative distribution function \(F\), then \[F(m)=?\]
If \(Q\) is the upper quartile of a continuous random variable \(X\) with cumulative distribution function \(F\), then \[F(Q)=?\]
Give the formula for the expected value of a function \(g(X)\) of a continuous random variable
(given in formulae book)
For a binomial distribution \(X\sim B(n,p)\), what is the formula for \(P(X=x)\)?
(given in formulae book)
For a Poisson distribution \(X\sim Po(\lambda)\), what is the formula for \(P(X=x)\)?
(given in formulae book)
Describe this shaded area using set notation in two ways
How is variance related to standard deviation?
\[X\sim B(n,p)\]
What values can \(X\) take?
\[X\sim Po(\lambda)\]
What values can \(X\) take?

 Verberge bekannte Karten
Verberge bekannte Karten