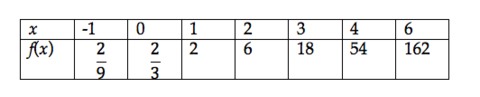
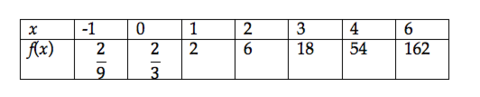
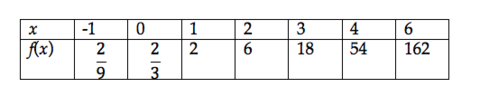
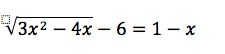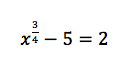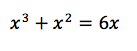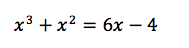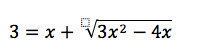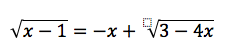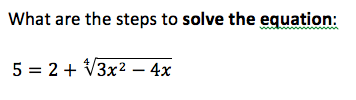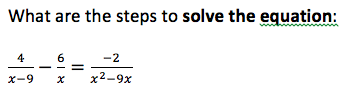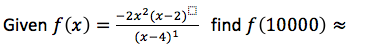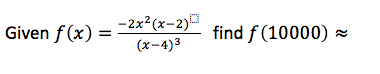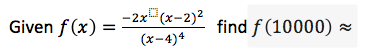12th grade Math Karteikarten am polynomials review, erstellt von Lance Erickson am 22/03/2017.
Angeheftet an
289
2
0
Keine Merkmale angegeben
|
|
Erstellt von Lance Erickson
vor mehr als 7 Jahre
|
|
Schließen