Terminos de principiantes antes de iniciar la materia
Pinned to
202
0
0
No tags specified
|
|
Created by Kevin Lascano
over 6 years ago
|
|
Close
|
|
Created by Kevin Lascano
over 6 years ago
|
|

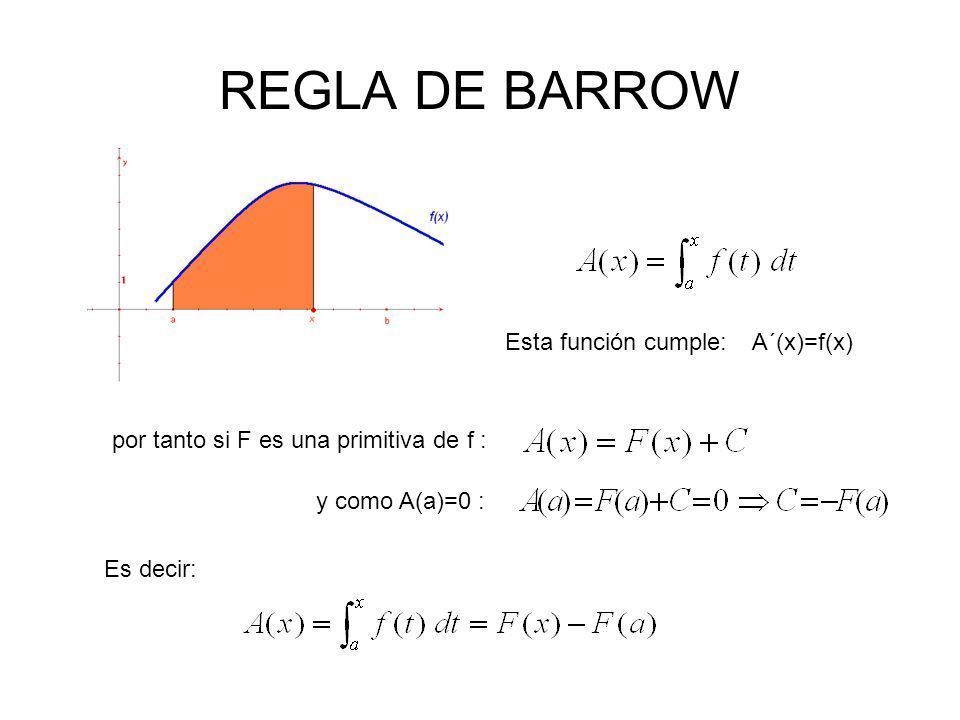
Regla de Barrow.
La importancia de la regla de Barrow es doble: es un método que permite calcular integrales definidas obteniendo únicamente una función tal que F’(x)=f(x) y calcularla en los límites de integración y representa una conexión entre Cálculo Diferencial y Cálculo Integral.
CONSTANTE DE INTEGRACION:
En cálculo, la integral indefinida de una función dada (es decir, el conjunto de todas
las primitivas de la función) se escribe siempre con una constante, la constante de
integración. Esta constante expresa una ambigüedad inherente a la construcción de
primitivas. Si una función f está definida en un intervalo y F es una primitiva de f,
entonces el conjunto de todas las primitivas de f viene dado por las funciones F (x) + C,
siendo C, una constante arbitraria.
La antiderivada
La integral es el proceso contrario a la derivada, la forma de identificar una integral es con el símbolo de integración que es el siguiente:
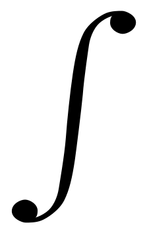
De manera general se pueden expresar como: d( ) de algo.
La antiderivada se expresa como, F(x),
Las integrales se dividen en dos
Integral definida
Integral indefinida
Veamos la (integral Indefinida)
Ahora siguiendo con el ejemplo: f(x)= 2x
Primero se escribe la integral, símbolo, función y
diferencial de x:
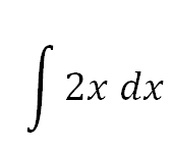
Se puede notar que el dos que está multiplicando con lo de arriba se puede simplificar con el dos que multiplica a todo lo de abajo quedando 1 multiplicando con x^2 por eso la solución es: x^2 más la constante de integración.
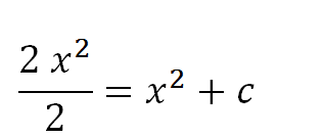

 Hide known cards
Hide known cards