Flashcards on Importancia y aplicación de la estadística, created by Albaro Cortes riveros on 13/05/2020.
|
Created by Albaro Cortes riveros
over 4 years ago
|
|
Close
|
|
Created by Albaro Cortes riveros
over 4 years ago
|
|
Estadística aplicada
"conjunto de procedimientos para reunir, medir, clasificar, codificar, computar, analizar y resumir información numérica adquirida sistemáticamente" (Ritchey, 2008: 1).
Funciones de la estadística
1. La descripción; el resumen de la información de tal modo que se pueda emplear mejor.
2. Y la inducción que consiste en formular generalizaciones a propósito de una determinada población sobre la base de una muestra extraída de la misma.
Importancia y aplicación de la estadística
• Radica en sus grandes aplicaciones en las diferentes actividades.
• Es de vital importancia en la toma de decisiones, ya que suministra la información necesaria para valorar planes y programas.
• Su adecuada utilización dependerá en especial del conocimiento, habilidad y experiencia de quién la emplea.
Clasificación de la estadística
• Descriptiva o deductiva: Se encarga de mostrar el resultado de los datos estudiados de forma específica.
• Inferencial o inductiva: Ofrece resultados junto con datos generales de investigación amplía.
• Aplicada: Proporciona resultados específicos y generalizados sobre la investigación.
• Matemática: Realiza los procesos de estadística deductiva o inferencial, y se utilizará el álgebra además de ciertos análisis más para ofrecer un punto de vista enfocado y formal.
Gráficas
Los datos numéricos obtenidos en un estudio estadístico pueden presentarse de forma visual a través de gráficas estadísticas, lo que hace que sean más fácilmente comprensibles.
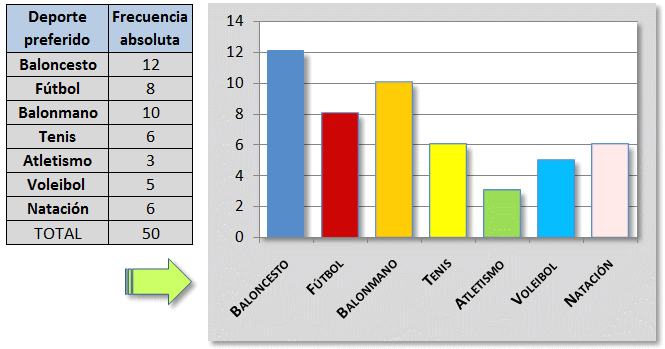
Para ello primero debemos tener nuestros datos acomodados en tablas de frecuencias.
Algunos tipos de graficas son:
• Diagrama de barras
Pasos de construcción:
1. Se construyen dos ejes.
2. En el eje horizontal, o eje de abscisas, se representan los datos o modalidades obtenidos.
3. En el eje vertical, eje de ordenadas, se representan con números las frecuencias de cada dato o modalidad.
4. Sobre el eje horizontal se levantan barras o rectángulos de igual base hasta la altura del valor numérico de la frecuencia de cada modalidad.
• Diagrama de sectores
En un diagrama de sectores cada dato viene representado mediante un sector circular cuyo ángulo es proporcional a su frecuencia absoluta.
1. El ángulo del sector se calcula dividiendo 360 (los grados de un círculo completo) entre el número de datos y multiplicando el resultado por la frecuencia de cada dato.
2. La fórmula para hallar estos cálculos es la siguiente:
Medidas de tendencia central para ubicar el dentro de los datos
• Media
• Mediana
• Moda
Clasificación de medidas
Asimetría
Sesgo : Denota la deformación horizontal de la curva
Mayor a cero, una cola más alargada hacia la derecha (positiva)
Menor a cero, con una cola más larga hacia la izquierda (negativa)
Curtosis:
Mayor a cero se le denomina leptocurtica (apuntamiento alto de la curva)
Igual a cero a este tipo de curva se le denomina mesocurtica (apuntamiento normal de la curva)
Menor a cero a este tipo de curva se le denomina platicurtica (apuntamiento bajo la curva).
