Problema puro de programación con enteros

Problema combinado de programación con enteros

PE binaria o PE 0 - 1

Relajación del PL de la PE

La región factible para cualquier PE debe estar contenida en la región factible para la relajación del PL correspondiente

Aún cuando la región factible para un PE es un subconjunto de la región factible para la relajación del PL del PE, el PE es mucho más difícil de resolver que la relajación del PL del PE.

Problema de la mochila

Cargo fijo

Ejemplo de planteamiento de restricciones:
De cuatro inversiones a lo más se puede invertir en dos

Si se invierte en la inversión 2 entonces también debe invertir en la 1

Si se invierte en la 2 no se puede invertir en la 4

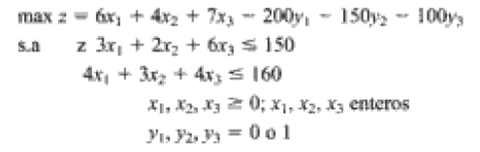
Solución de PE con LINDO

Precios sombra y costos reducidos en un PE de LINDO

Después de END lo que se escribe por cada variable x 0 - 1

Si w pudiera asumir los valores 0,1,2,. . . , después de END se escribe

Comando para señalar a LINDO que las primeras n variables que aparecen en la formulación podrían asumir cualquier valor entero no negativo

Capítulo 9.3

Si al resolver la relajación del PL de un PE puro se obtiene una solución con todas las variables enteras entonces . . .

Nombre que recibe el valor óptimo de z para la relajación del PL

CONCEPTOS DE:
1) Árbol
2) Nodo
3) Arco

Regla LIFO

Solución Probable

Aspectos claves del método de ramificación y acotamiento para PE puros

1) Las tres situaciones que dan como resultado un subproblema que ya está terminado

2) Situaciones en las que se deja de considerar un subproblema

relación de dependencia

Método de corte

¿Cómo se genera el plano cortante?

Enumeración Implícita

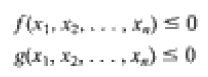
Restricción si . . . entonces

Formulación para una restricción si . . . entonces