GCSE Math Flashcards on All math revision, created by katiehumphrey on 16/01/2014.
Pinned to
458
27
0
|
|
Created by katiehumphrey
almost 11 years ago
|
|
Close
|
|
Created by katiehumphrey
almost 11 years ago
|
|

direct proportion
If two quantities are in direct proportion, as one increases, the other increases by the same percentage.
If y is directly proportional to x, this can be written as y ∝ x
indirect proportion
Inverse proportion is when one value increases as the other value decreases.
Straight line
y ∝ x
y = kx
This equation gives us a straight line. The gradient of the line is k.
Quadratic
y ∝ x2
y = kx2
This equation gives us a curve. The larger the value of k, the steeper the graph.
Cubic
y ∝ x3
y = kx3
Square root
y ∝square root of x
y = ksquare root of x
You have similar shaped curves for any powers between 0 and 1. Again, increasing k will make the graph steeper.
Inverse proportion
y ∝ 1/x ²
y = k/x ²
Inverse proportion leads to curved graphs.
surds
square root of ab = square root of a x square root of b
square root of a x square root of a = a
equations with fractions
graph transformations
f(x) + a [0/a]
f(+ ) = left f(x- ) = right
2f(x) = y coordinates x 2
-f(x) = reflection of f(x)
f(2x) = 1/2 x coordinate
sin cos tan graphs
factorising
quadratic equations
To solve a quadratic equation, the first step is to write it in the form: ax2 + bx + c = 0. Then factorise the equation
completing the square
This is another way to solve a quadratic equation if the equation will not factorise.
It is often convenient to write an algebraic expression as a square plus another term. The other term is found by dividing the coefficient of x by 2, and squaring it.
quadratic formula
Solve 2x2 - 5x - 6 = 0
Here a = 2, b = -5, c = -6
the quadratic formula

A taxi firm charges £0.50 per mile plus a fixed charge of £2.00. Write down a formula for the cost (C) of hiring this taxi to travel 'n' miles.
Collecting like terms
To simplify an expression, we collect like terms.
Look at the expression: 4x + 5x -2 - 2x + 7
(2x + 5) squared
multiplying out brackets
Multiply out: 3(4x - 7)
multiplying out negatives
Multiply out the expression:
-3(2n - 8)
multiplying out 2 brackets
Multiply out these two brackets:
(x + 4) (x + 3)
FOIL
first outer inner last
proof
prove
(3n + 1) squared - (3n - 1) squared
is a multiple of 6
Index notation:
used to represent powers
index multiplying and dividing
solving equations
solving inverse equations
Here is how to solve 2a + 3 = 7 using inverses.
unknowns on both sides of the equation
Solve the equation 3b + 4 = b + 12, and find the value of b.
equations with brackets
Solve the equation: 3(b + 2) = 15
trial and improvement
Find the answer to the equation x3 – 2x = 25 to one decimal place.
simultaneous equations
solving inequalities
Solve the expression 3x - 7 < 8
double inequalities
Solve the inequality -4 < 2x - 6 < 12
equations for a straight line graph can contain
tables for graph plotting
On a graph, parallel lines have the same gradient.
For example, y = 2x + 3 and y = 2x - 4 are parallel because they both have a gradient of 2.
the lines y = 2x + 3 and y = -1/2 x -1 cross at right angles
y = mx + c
m = gradient
c = y intercept
cubic graphs
Calculate the points and then plot the graph for the equation y = x3 - x + 8
reciprocal graphs
Graphs of the form y = 1/x, 2/x, 3/x
quadratic sequences
If the difference between the terms changes, this is called a quadratic sequence.
If you use the formula n^2 + n to make a sequence, it means that:
When n = 1 you get 1^2 + 1 = 2
When n = 2 you get 2^2 + 2 = 6
When n = 3 you get 3^2 + 3 = 12
When n = 4 you get 4^2 + 4 = 20
- giving the sequence 2, 6, 12, 20.
histograms
frequency density = frequency / class width
frequency tables
finding the mean and median
frequency polygons
dot in midpoint
median upper quartile lower quartile and interquartile range of frequency
stem and leaf diagram

box plots
Amit is 12 years old. His brother, Arun, is 9.
Their grandfather gives them £140, which is to be divided between them in the ratio of their ages. How much does each of them get?
standard form
adding and subtracting standard form
multiplying and dividing standard form
parts of a circle
circumference of a circle
area of a circle
area of a semi circle
perimeter of a semi circle
circle theorems
angle at the centre of a circle
angles in the same segment are equal
angles in a semi circle are 90 degrees
The angle at the centre (AOB) is twice the angle at the circumference (APB). As AOB is 180°, it follows that APB is 90°
Opposite angles in a cyclic quadrilateral add up to 180°
A cyclic quadrilateral is a quadrilateral whose vertices all touch the circumference of a circle. The opposite angles add up to 180o.
In the cyclic quadrilateral below, angles A + C = 180o, and angles B + D = 180o
The angle between the tangent and radius is 90°
A tangent to a circle is a line which just touches the circle.
difficult circle theorem
quadrilateral has been divided into two triangles, so the interior angles add up to 2 × 180 = 360°.
interior angles of polygons
The volume of a pyramid is:
1/3 × base area × perpendicular height
The surface area of a pyramid is the area of the base + the area of all the other sides.
The volume of a cone is:
1/3πr^2h
The curved surface area of a cone is:
πrL
(where L is the slant height).
Note this doesn't include the area of the base, which is a circle, area πr^2.
The volume of a sphere is
4/3πr^3
The surface area of a sphere is:
4πr^2
volume and area
3 figure bearings
Pythagoras
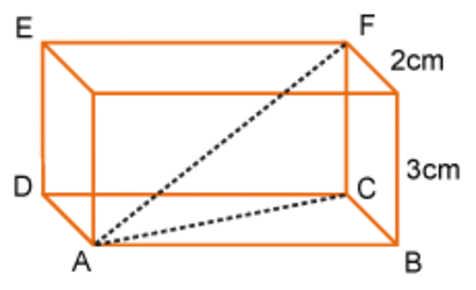
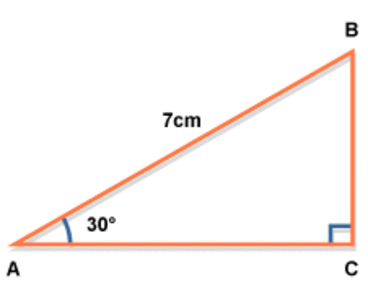

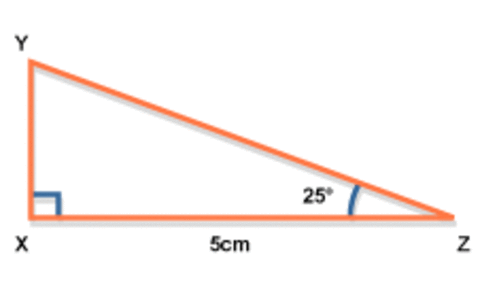

the sine rule
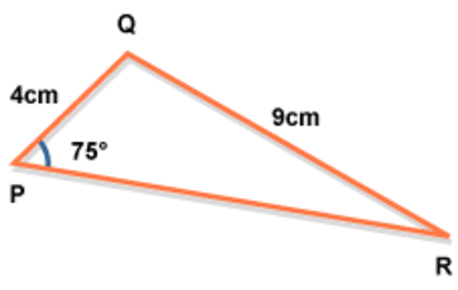
the cosine rule
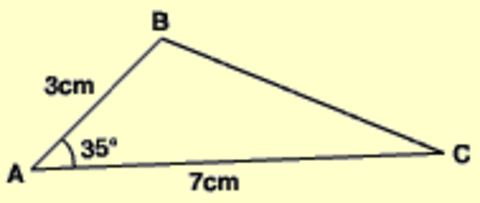
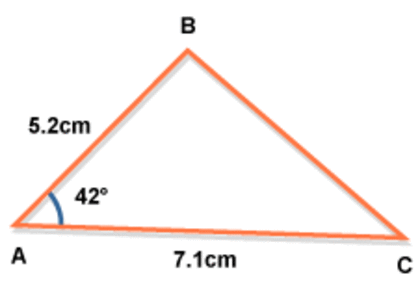
area of a triangle

 Hide known cards
Hide known cards