Key points and important formulae for the WJEC GCE Maths C1 module
Pinned to
138
4
0
No tags specified
|
|
Created by Daniel Cox
over 8 years ago
|
|
Close
|
|
Created by Daniel Cox
over 8 years ago
|
|

Formula for the gradient of a line joining two points
The quadratic equation formula for solving \[ax^2+bx+c=0\]
The midpoint of \( (x_1, y_1) \) and \( (x_2, y_2) \) is...
A line has gradient \(m\).
A line perpendicular to this will have a gradient of...
If we know the gradient of a line and a point on the line, a formula to work out the equation of the line is...
Formula for the distance between two points...
To find where two graphs intersect each other...
In a right-angled triangle,
\[ \cos{\theta}=... \]
In a right-angled triangle,
\[ \sin{\theta}=... \]
In a right-angled triangle,
\[ \tan{\theta}=... \]
To simplify \( \frac{a}{\sqrt{b}} \)...
(a.k.a. 'rationalising the denominator')
To simplify \( \frac{a}{b+\sqrt{c}} \)...
(a.k.a. 'rationalising the denominator')
\[\left(\sqrt{m} \right)^{3}=... \]
\[\sqrt{a}\times \sqrt{b}=...\]
\[\frac{\sqrt{a}}{\sqrt{b}}=...\]
To find the gradient of a curve at any point, use...
Parallel lines have the same...
To find the gradient of the line \(ax+by+c=0\)...
Where is the vertex of the graph \[y=\left ( x+a \right )^2+b\]?
The discriminant of \(ax^2+bx+c\) is...
The discriminant of a quadratic equation tells us...
If a quadratic equation has two distinct real roots, what do we know about the discriminant?
If a quadratic equation has two equal roots, what do we know about the discriminant?
If a quadratic equation has no real roots, what do we know about the discriminant?
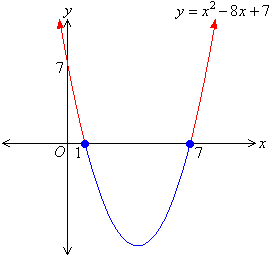
Here is the graph of \(y=x^2-8x+7\).
Use it to solve the quadratic inequality \(x^2-8x+7>0\)
The formula for differentiating by first principles...
If \(y=ax^n\),
then \(\frac{dy}{dx} =...\)
If \(\left (x+a \right )\) is a factor of \(f(x)\), then...
If the remainder, when \(f(x)\) is divided by \((x+a)\) is R, then...
What effect will the transformation \(y=f(x)+a\) have on the graph of \(y=f(x)\)?
What effect will the transformation \(y=f(x+a)\) have on the graph of \(y=f(x)\)?
What effect will the transformation \(y=af(x)\) have on the graph of \(y=f(x)\)?
What effect will the transformation \(y=f(ax)\) have on the graph of \(y=f(x)\)?
How would you use the second derivative, \(\frac{d^2 y}{dx^2}\) to determine the nature of the stationary points on a graph?
A function is said to be 'increasing' when its gradient is...
A function is said to be 'decreasing' when its gradient is...
\[a^0=?\]
\[a^m \times a^n = ?\]
\[a^m \div a^n = ?\]
\[\left( a^m \right) ^n=?\]
\[a^{-n}=?\]
\[a^{\frac{m}{n}}=?\]
What does \(n!\) mean?

 Hide known cards
Hide known cards