Cuando un polinomio es igual a cierto valor (ya sea un entero u otro polinomio), el resultado es una ecuación.

Podemos resolver estas ecuaciones cuadráticas usando las reglas del álgebra, aplicando técnicas de factorización donde sea necesario, y usando la Propiedad Cero de la Multiplicación.

Esta propiedad puede parecer obvia, pero tiene importante implicaciones en cómo resolvemos ecuaciones cuadráticas: significa que si tenemos un polinomio factorizado igual a 0, podemos estar seguros de que al menos uno de sus factores es también 0.

La ecuación 5a² + 15a = 0 es una ecuación cuadrática porque puede escribirse como 5a² + 15a + 0 = 0, que es equivalente a la forma ax² + bx + c = 0, con c = 0.

Aquí es donde usamos la Propiedad Cero de la Multiplicación.

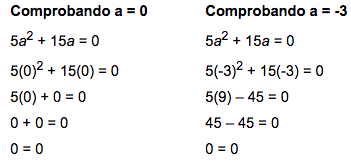
Esta ecuación cuadrática, 5a² + 15a = 0, tiene dos raíces: 0 y -3. Podemos usar el Producto Cero de la Multiplicación para resolver ecuaciones cuadráticas de la forma ax² + bx + c = 0. Primero factorizamos la expresión, y luego resolvemos cada una de las raíces.

Cuando usamos la Propiedad Cero de la Multiplicación para resolver una ecuación cuadrática, necesitamos asegurarnos que la ecuación este igualada a cero. Algunas veces esto requerirá de mover los términos para que quede 0 en un lado de la ecuación.