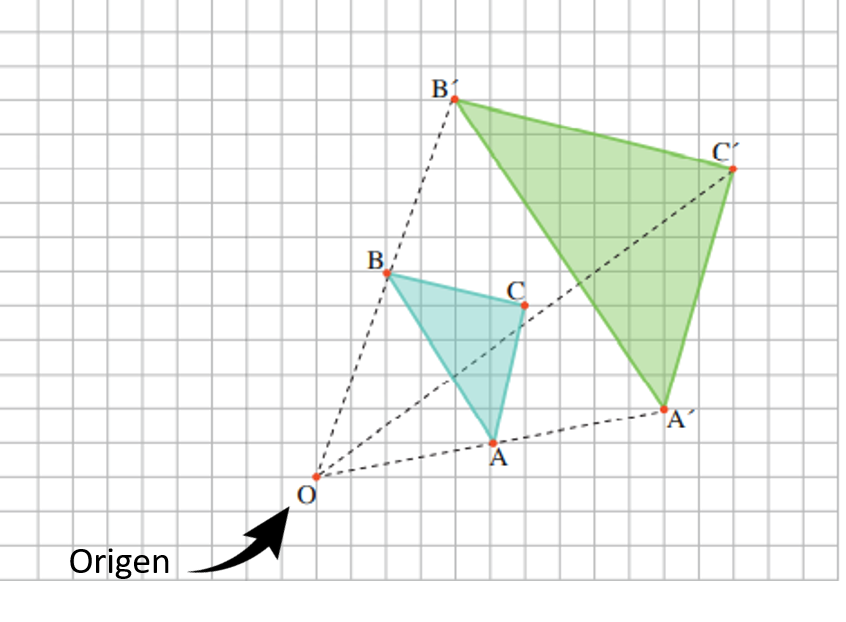
Se estudiarán las transformaciones o cambios que se le pueden realizar a polígonos representados en el plano cartesiano
Pineado a
8
0
0
Sin etiquetas
|
|
Creado por Diana Ramgo
hace más de 3 años
|
|
Cerrar